天美講堂丨如何確定熒光壽命?
要點簡介
我們可以通過分析光致發光或熒光衰減來獲得壽命。在擬合衰減時,必須考慮樣品潛在的光物理過程,來評估擬合是否適當。本文,我們將使用Fluoracle?軟件來對熒光衰減進行單指數、多指數和非指數擬合。
●?不同壽命的發射體系可能是由于樣品本身的原因。
●?平均壽命可以用振幅或強度加權平均壽命來描述。
●?可以通過軟件對擬合結果進行優化,但應根據體系潛在的光物理過程來評估是否合適。
激發態總體
通過時間相關單光子計數得到激發態分布[M*]。激發態分子濃度[M*]在時間t的衰減為:

其中,[M*]0是在時間為0時處于激發態分子的濃度。t = 0相當于使用TCSPC時激發脈沖的到達時間。存在多種相互競爭的衰減過程,分別為輻射和非輻射途徑。與這些參數相關的速率常數是kr和knr,分別是輻射衰減和非輻射衰減之和的速率常數。用k來表示所有速率常數的總和。
然而,我們不能直接測試激發態分子的濃度。相反,可測試的參數是熒光強度I。在時間t的熒光強度如方程2所示。

其中τ是熒光壽命。τ與速率常數的關系如下:

如何擬合單指數衰減
最簡單的熒光衰減為單指數衰減:

其中t是時間,τ是熒光壽命,B是指前因子。熒光壽命定義為強度降至初始值的1/e(=0.368)所需的時間(圖1a)。熒光衰減通常以對數坐標顯示,對數坐標給出了單指數衰減的線性關系(圖1b)。

圖1(a)在線性坐標上的的熒光衰減;(b)在對數坐標上的的熒光衰減。1
擬合方法:
必須用適當的函數對熒光衰減進行擬合。TCSPC數據的擬合有兩種常用方法,尾部擬合和解卷積擬合。在多次迭代后,壽命和B指前因子會發生變化,以優化擬合。
擬合評估:
可以通過計算X2來評估擬合。通過原始數據點和擬合點之間的差異,以量化數據擬合的效果。測量的熒光衰減函數N(tk)和計算的衰減函數NC(tk)之間的差值通過數據點的數量n進行評估。

X2值為1表示通過擬合。如果值高于1.2,則表明擬合不能很好地描述此衰減。可接受的X2在不同體系中有所不同,其與噪聲相關。在測試樣品熒光衰減之前需要確定單組分熒光團,以確定體系可實現的靈敏度。
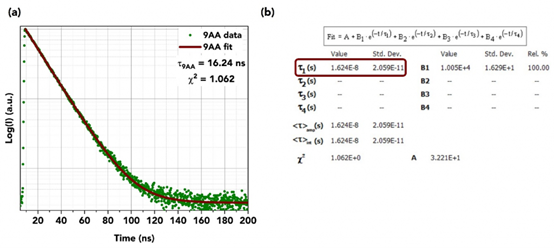
圖2 (a)使用穩態瞬態熒光光譜儀FS5測試的9AA的熒光衰減;(b)Fluoracle?軟件中的單指數擬合分析。
圖中τ是通過將單個指數尾部擬合到Fluoracle?中來確定的。Fluoracle?軟件通過調整τ和B的值,直到獲得具有最低殘差的最小二乘擬合,即16.2?ns(圖2b)。
如何擬合多指數衰減
當樣品含有多個熒光團,或單個分子具有多個熒光發射體系(如構象異構體或互變異構體)時,必須使用多指數模型:其中I(t)是作為時間函數t的熒光強度,歸一化為t=0時的強度,τi是第i個衰變組分的熒光壽命,Bi是該組分的分數振幅。

理論上,模型中可以包含的指數分量的數量沒有限制。可以通過增加熒光組分的數量來實現更好的擬合,但要符合樣品實際的光物理過程。為了使壽命組分有意義,它們必須代表樣品中發生的不同光物理過程,因此應根據預期光物理過程來確定熒光組分的數量。
多指數衰減的一個例子是熱激活延遲熒光(TADF)材料。TADF材料熒光衰減為雙指數擬合。如圖3a所示,可以用兩個指數衰減來精確擬合,τ1=65 ns和τ2=?1061 ns,其對應材料S1激發態的即時熒光和延遲熒光。

圖3 (a) 使用穩態瞬態熒光光譜儀FS5測量的TADF的雙指數熒光衰減;(b)Fluoracle?中的擬合結果。
如何擬合非指數衰減
有許多樣品類型不遵循指數衰減行為。無機材料(包括半導體和量子點等體系)的光致發光衰減通常就是這種情況。非指數衰減的一個例子是涂有硫化鋅層(InP/ZnS)的磷化銦量子點的光致發光,如圖4所示。
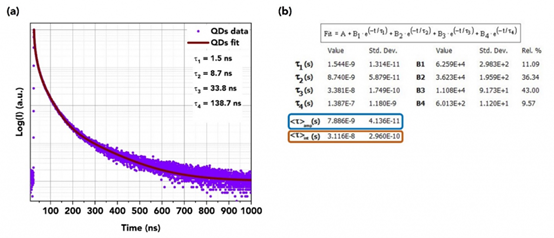
圖4 (a) 使用穩態瞬態熒光光譜儀FS5測量的InP/ZnS量子點的光致發光衰減;
(b)Fluoracle?中相應的擬合分析,其中突出顯示了振幅加權平均壽命(藍色框)和強度加權平均壽命(橙色框)。
平均壽命
Fluoracle?軟件中顯示了兩種平均壽命,因為平均壽命有不止一個定義。文獻中最常報道的兩種平均壽命是振幅加權平均壽命和強度加權平均壽命。需要事先了解材料衰減的內在機制,才能選擇應該使用的平均壽命。
振幅平均壽命<τ>amp,通過其分數振幅(Bi)對每個壽命組分(τi)進行加權:4

其中:

振幅平均壽命是穩定狀態下熒光團的特征,并且在數學上與速率常數相關。3振幅平均壽命通常用于熒光團之間發生能量轉移的生物系統中。因此,由于其異質性及其與周圍環境的相互作用,其壽命衰減是多指數的。
強度平均壽命加權每個壽命分量(τi)乘以該分量的分數強度(Biτi)4:

強度平均值更加強調較長的壽命,降低了分數振幅變化和較短壽命的可見性。這使得平均值在擬合過程中對熒光組分數量的變化顯得更加穩定。2強度平均壽命適用于例如發射體系的集合,例如嵌入光子晶體中的量子點,以及熒光依賴于納米晶體尺寸的半導體納米晶體。5相同材料但不同尺寸的納米晶體將以不同的波長發射,因此,應考慮納米晶體的整個激發體系的平均壽命。
了解您的樣品
擬合最好通過仔細評估體系中的光物理過程來評估,而數學計算的“最優”解并不總是合適的。以與非指數QD系統相同的方式處理單組分稀土樣品為例,應該始終根據樣品本身特性來決定擬合方法。擬合在很大程度上取決于用戶輸入的值(擬合范圍、背景、建議使用壽命)。擬合結果受這些值的微小變化的影響很大,這些變化將對最終擬合產生無法計算的影響。
總結
本文探討了擬合單個樣品熒光衰減的基本原理。為了提高對體系的理解,可以一起分析多個衰減函數。對熒光衰減的擬合,應始終考慮樣品潛在的光物理過程,根據樣品本身特性確定擬合方式。愛丁堡一體化穩態瞬態熒光光譜儀FS5可使用Fluoracle?軟件對樣品進行單指數、多指數或非指數擬合,滿足多樣化樣品擬合需求。

參考文獻
1. D. M. Jameson, Introduction to Fluorescence, 2014.
2. E. Fi?erová and M. Kubala, Mean fluorescence lifetime and its error, J Lumin, 2012, 132, 2059–2064.
3. A. Sillen and Y. Engelborghs, The Correct Use of ‘Average’ Fluorescence Parameters, Photochem Photobiol, 1998, 67, 475–486.
4. B. Valeur and M. N. Berberan-Santos, Molecular Fluorescence, Wiley-VCH, 2nd edn., 2012.
5. G. Zatryb and M. M. Klak, On the choice of proper average lifetime formula for an ensemble of emitters showing non-single exponential photoluminescence decay, Journal of Physics Condensed Matter, DOI:10.1088/1361-648X/ab9bcc.

天美分析更多資訊























