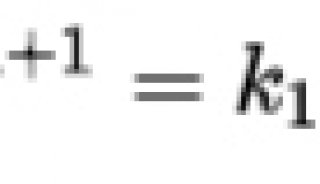檢測數據處理基礎知識-2
3. 隨機誤差規律性
(1)小誤差出現的概率比大誤差多,特別大的誤差出現的概率極少。
(2)正誤差和負誤差出現的概率是相等的。
4. 標準正態分布:
橫坐標用u表示,其定義式為:
即:以σ為單位來表示隨機誤差。
函數表達式為:
因此曲線的形狀與σ大小無關, 不同的曲線都合并為一條。
記作N(0,1)
隨機誤差的區間概率
1. 定義
隨機誤差在某一區間出現的概率以某段正態分布曲線下所包含的面積表示。
一條完整的正態分布曲線所包含的面積,表示所有測量值出現的概率的總和,即是100%,等于1。用算式表示為:
一般以 為單位,計算不同 值曲線所包含的面積,制成概率積分表供直接查閱。
2. 計算公式
概率=面積=
?
有限數據的統計處理
隨機誤差分布的規律給數據處理提供了理論基礎,但它是對無限多次測量而言。實際工作中我們只做有限次測量,并把它看作是從無限總體中隨機抽出的一部分,稱之為樣本。樣本中包含的個數叫樣本容量,用n表示。
數據的趨勢 → 數據集中趨勢的表示
1. 算術平均值
n次測定數據的平均值。
是總體平均值的最佳估計。對于有限次測定,測量值總朝算術平均值 集中,即數值出現在算術平均值周圍;對于無限次測定,即n → ∞時, →μ。
2. 中位數M
將數據按大小順序排列,位于正中間的數據稱為中位數M。
n為奇數時,居中者即是;n為偶數時,正中間兩個數據的平均值即是。
數據的趨勢 → 數據分散程度的表示
1. 極差R(或稱全距):指一組平行測定數據中最大者(Xmax)和最小者(Xmin)之差。
R = Xmax - Xmin
2. 平均偏差:各次測量值與平均值的偏差的絕對值的平均。
絕對偏差 di = Xi - (i =1,2,…,n )
平均偏差
相對平均偏差
3. 標準偏差S:計算方法
標準偏差S =
相對標準偏差,也叫變異系數,用CV表示,一般計算百分率。
相對標準偏差RSD = ×100 %
自由度f:f = n-1
平均值的置信度區間 → 定 義
1. 置信度
置信度表示對所做判斷有把握的程度。 表示符號:P 。
有時我們對某一件事會說“我對這個事有八成的把握”。這里的“八成把握”就是置信度,實際是指某事件出現的概率。
常用置信度:P=0.90,P=0.95;或P=90%,P=95%。
2. 置信度區間
按照t分布計算,在某一置信度下以個別測量值為中心的包含有真值的范圍,叫個別測量值的置信度區間。
1. t的定義
,與 對比。
2. t分布曲線
(1) t分布曲線:t分布曲線的縱坐標是概率密度,橫坐標是t,這時隨機誤差不按正態分布,而是按t分布。
(2) 與正態分布關系:t分布曲線隨自由度f變化,當n→∞時,t分布曲線即是正態分布。
t分布曲線
【t分布值表】
由表可知,當f→∞ 時,S→σ,t即是u。
實際上,當f=20時,t與u已十分接近。
3. 平均值的置信度區間:
(1) 表示方法:
(2) 含義:在一定置信度下,以平均值為中心,包括總體平均值的置信度區間。
(3) 計算方法:
① 求出測量值的 ,S,n。
② 根據要求的置信度與f值,從t分布值表中查出t值。
③ 代入公式計算。
?
顯著性檢驗 → 平均值與標準值比較
常用的方法有兩種:t檢驗法和F檢驗法。
分析工作中常遇到兩種情況:樣品測定平均值和樣品標準值不一致;兩組測定數據的平均值不一致。需要分別進行平均值與標準值比較和兩組平均值的比較。